Deciding whether to reject a part or not based on a quality measurement always carries with it a finite risk: you could unknowingly decide that a perfectly good part is actually bad (a Type 1 error), or you might incorrectly conclude that a bad part is actually good (a Type 2 error). There is a different kind of cost associated with each of these errors. The risk of committing one of these errors is minimized by basing the decision on more than one measurement. However, it’s important for efficiency’s sake to take no more measurements than necessary. In this post, we discuss how to precisely calculate the optimal number of measurements to conduct in order to make a part quality decision.
4 Possible Scenarios When Deciding Whether to Accept or Reject a Part
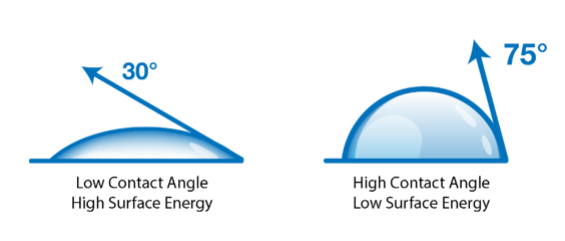
One of the primary goals of quality inspection is to determine if parts are good or bad. We make this decision based on some kind of measurement. This could be a dimensional measurement, a measurement of gloss, package weight, etc. For the examples here, we will use contact angle measurements that sense a surface chemistry characteristic that affects the adhesion of paints, coatings, or adhesives, such as treatment level or presence of contamination. For quality inspections, there is generally a range of measured values that correspond to an acceptable part, and any measurement outside of this range would trigger part rejection or rework.
There are four distinct scenarios that can result from making a decision regarding quality based on a measurement. Only two of them are the desired result of a quality inspection:
- The part is accepted based on the measurement, and it was indeed actually within the specifications
- The part is rejected based on the measurement, and it was actually outside of acceptable limits
However, there are also two ways in which we can make an incorrect decision regarding part quality:
- The part is rejected based on the measurement, but it is actually a perfectly good part
- The part is actually bad but is incorrectly accepted as being good
These incorrect decisions are called errors; the first one (incorrectly rejecting a good part) is called a Type 1 error, while the second one (incorrectly accepting a bad part) is called a Type 2 error. This Table shows the relationship between these errors and the measurement process:
The Significance of Type I Errors and Type II Errors to Your Business is Different
Committing a Type I error (the incorrect rejection of a perfectly good part) incurs an economic cost: you are throwing away or reworking something that didn’t need it, and it reduces the economic efficiency of the manufacturing operation.
Type II errors are more insidious. They occur when a substandard part is incorrectly accepted and either passed on to the next manufacturing step or, in the case of a final inspection, sent to a customer. This is a product quality error, and the costs can be very high for committing this kind of error. Imagine sending a poorly treated part onto an adhesive bonding operation: the final structure may fail in the customer’s hands. A painted product may peel and corrode prematurely, and an improperly cleaned medical device could cause serious harm to a patient. The results include damage to reputation and brand perception, along with the possibility of product recalls or product liability issues.
How to Minimize Quality Risks in Manufacturing While Maximizing Efficiency
One approach to avoid committing Type 1 or Type 2 errors is simply to increase the number of inspections per part. But each additional inspection requires time and effort, which adds to manufacturing costs, so it’s important only to take the minimum number of inspections required to get the desired level of confidence in the outcome of the quality inspection. It’s a straightforward process to make this calculation that we’ll walk through. Making this calculation requires the following information about the measurements and the process:
- The mean and standard deviation of the quality metric for parts that are considered to be of acceptable quality. For example, a correctly functioning machining process creates parts with a mean diameter of 5.00 mm with a standard deviation of 0.05 mm; or a plasma treatment process for an injection molded polyethylene part results in an average water contact angle of 35° with a standard deviation of 2°.
- The deviation from this means that it constitutes an unacceptable part. For example, while the mean contact angle of well-treated parts is 35°, as long as the actual contact angle is within ±5° of the nominal value, the parts function perfectly well. Parts with an actual contact angle that deviate more than ±5° from the mean show diminished adhesion and are unacceptable.
- The risk that you (the manufacturer) are willing to assume for making a Type 1 error
- The acceptable risk for making a Type 2 error.
While values for the expected and acceptable values of the quality metric are usually straightforward to determine, defining the acceptable risk for making an error requires a bit of thought. Remember that the more risk we are willing to assume, the fewer measurements need to be made to arrive at a quality decision. The lower our risk tolerance, the more measurements we will need to take.
Let’s start by considering the acceptable risk for committing a Type 1 error. If we set this to a value of 0.01, what this means is out of every 100 good parts we inspect, we will, on average, reject one of them incorrectly. In other words, we will be incorrectly discarding or sending back for rework about 1 out of every 100 parts (remember this value can be set to any level that is acceptable to the manufacturer). The incorrectly rejected parts represent an economic cost to the manufacturing process.
Rethink your adhesion manufacturing processes with Surface Intelligence.
Now consider setting the acceptable risk for committing a Type 2 error. This is where a part of unacceptable quality is incorrectly identified as good. We might set this to a value of 0.001, which means that out of every 1000 bad parts that are inspected, on average, one of them will be incorrectly accepted. This is not as bad as it might sound: if only 1 out of every 1000 parts produced is bad, then there will be only one incorrectly accepted bad part out of every 1,000,000 parts produced.
Once these parameters are determined, it is a straightforward calculation to determine the exact number of inspections required to accept or reject parts based on known and acceptable risk values. This value is usually small and frequently no more than a few. The payback in economic terms and in reduced liability for taking a few more than just one measurement per part can be significant.
Learn more about water contact angle and how you can gain critical insights and drive manufacturing and supply chain innovation by downloading the eBook "What is Contact Angle?"